La resolución gráfica como punto de partida en optimización lineal

La optimización lineal es una herramienta fundamental para modelar y resolver problemas de toma de decisiones, desde la planificación de la producción hasta la asignación eficiente de recursos.

Aunque los problemas reales suelen involucrar un gran número de variables, el caso de dos variables de decisión desempeña un papel clave desde el punto de vista pedagógico. En este contexto, el método gráfico permite ver literalmente el problema: qué soluciones son posibles, dónde están las restricciones y por qué ciertas soluciones son mejores que otras.

El método gráfico consiste en representar cada restricción como una región del plano y observar qué puntos cumplen todas ellas simultáneamente. De esta forma, el problema abstracto se convierte en una figura geométrica concreta, lo que facilita enormemente la comprensión del concepto de solución óptima.

Formulación del problema

Un problema de optimización lineal con dos variables puede escribirse como:

• Función objetivo: \(\max\; z = c_1 x_1 + c_2 x_2\) o \(\min\; z = c_1 x_1 + c_2 x_2\).

• Sujeto a un conjunto de restricciones lineales: \(a_{i1} x_1 + a_{i2} x_2 \leqslant b_i, \; \forall i = 1, \dots, m\).

• Variables de decisión: \(x_1, x_2\) que con frecuencia son no negativas, es decir \(x_1, x_2 \geqslant 0\).

El objetivo es encontrar los valores de las variables de decisión, $x_1$ y $x_2$, que optimicen la función objetivo cumpliendo todas las restricciones.

Representación gráfica de las restricciones y región factible

Intuitivamente, la región factible recoge todas las decisiones que son posibles desde el punto de vista del problema planteado.

Cada restricción lineal define un semiplano en el plano $\mathbb{R}^2$. Para representar una restricción gráficamente:

1. Dibuja la recta correspondiente a la igualdad.
2. Determina qué lado de la recta cumple la desigualdad.
3. Sombrea el semiplano factible.

Las restricciones de no negatividad, en caso de existir, limitan la solución al primer cuadrante.

La región factible es la intersección de todos los semiplanos definidos por las restricciones.

Desde el punto de vista geométrico, esta región presenta una serie de propiedades fundamentales.

• La región factible es un conjunto convexo.
• La región factible puede estar acotada o no acotada. En caso de estar acotada, la región factible es un polígono.
• Toda solución factible se encuentra dentro o sobre el límite de esta región.

Si la región factible es vacía, se dice que el problema es infactible, es decir, no hay ninguna solución que verifique todas las restricciones impuestas al problema.

Función objetivo y optimalidad

La función objetivo puede interpretarse como una familia de rectas paralelas:

\[z := c_1 x_1 + c_2 x_2 = k\]

donde cada valor de $k$ corresponde a una recta diferente. Maximizar (o minimizar) la función objetivo $z$ consiste en mover esta recta en la dirección de mejora definida por los coeficientes de la función objetivo mientras siga intersecándose con la región factible.

Gráficamente, la solución óptima se encuentra donde la recta de la función objetivo toca por última vez la región factible. Esto suele ocurrir en un vértice o punto extremo, aunque pueden existir múltiples soluciones óptimas a lo largo de un borde, ya sea un segmento (región acotada) o una semirrecta (región no acotada).

Este razonamiento geométrico conduce a un resultado fundamental de la optimización lineal:

Si existe una solución óptima, entonces al menos una solución óptima se encuentra en un vértice de la región factible.

Pueden surgir varias situaciones:

• Solución óptima única: la función objetivo, en su óptimo, toca la región factible en un solo vértice.
• Múltiples soluciones óptimas:
  • Región acotada: la función objetivo, en su óptimo, es coincidente con un segmento en el borde de la región factible, es decir, un lado del polígono.
  • Región no acotada: la función objetivo, en su óptimo, es coincidente con una semirrecta en el borde de la región factible (es necesario que la región factible no esté acotada).
• Solución óptima no acotada: la función objetivo puede mejorar indefinidamente.
• Problema infactible: no existe solución, es decir, la región factible es vacía.

Es importante señalar que en problemas reales es muy difícil encontrar regiones factibles no acotadas, ya que las variables de decisión suelen estar relacionadas con recursos o decisiones que están acotadas por ser finitos.

Ejemplos ilustrativos

Con el objetivo de mostrar las distintas situaciones, se presentan a continuación los siguientes ejemplos ilustrativos, indicando su formulación matemática y su resolución gráfica de forma dinámica.

Solución óptima única

Sea el siguiente problema de optimización lineal:

\[\begin{aligned} \max\;\;& z = 6x_1 + 3x_2 \\ \text{s. a:}\;\;& 2x_1 + 4x_2 \leqslant 8 \\ & -x_1 + 4x_2 \leqslant 4 \\ & x_1 - x_2 \leqslant 2 \\ & x_1, x_2 \geqslant 0 \end{aligned}\]

En la siguiente animación se observa cómo se construye progresivamente la región factible y cómo la recta de la función objetivo se desplaza hasta alcanzar el óptimo en un vértice.

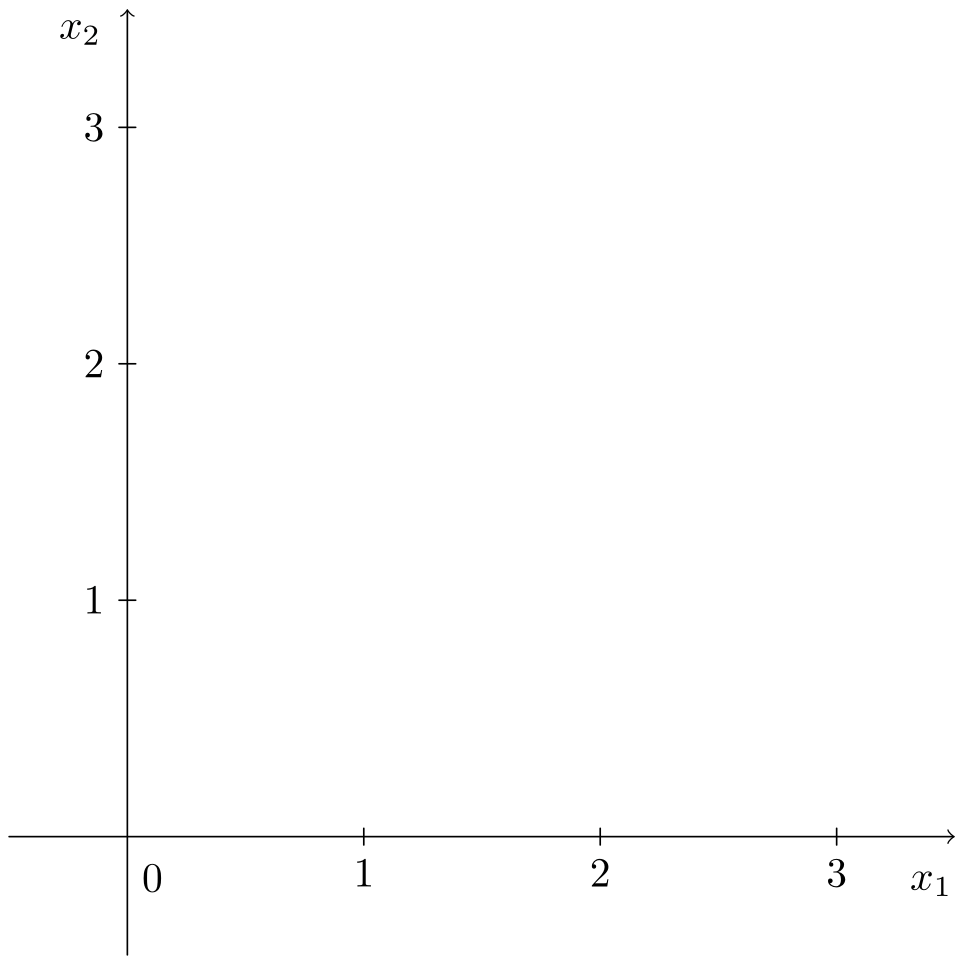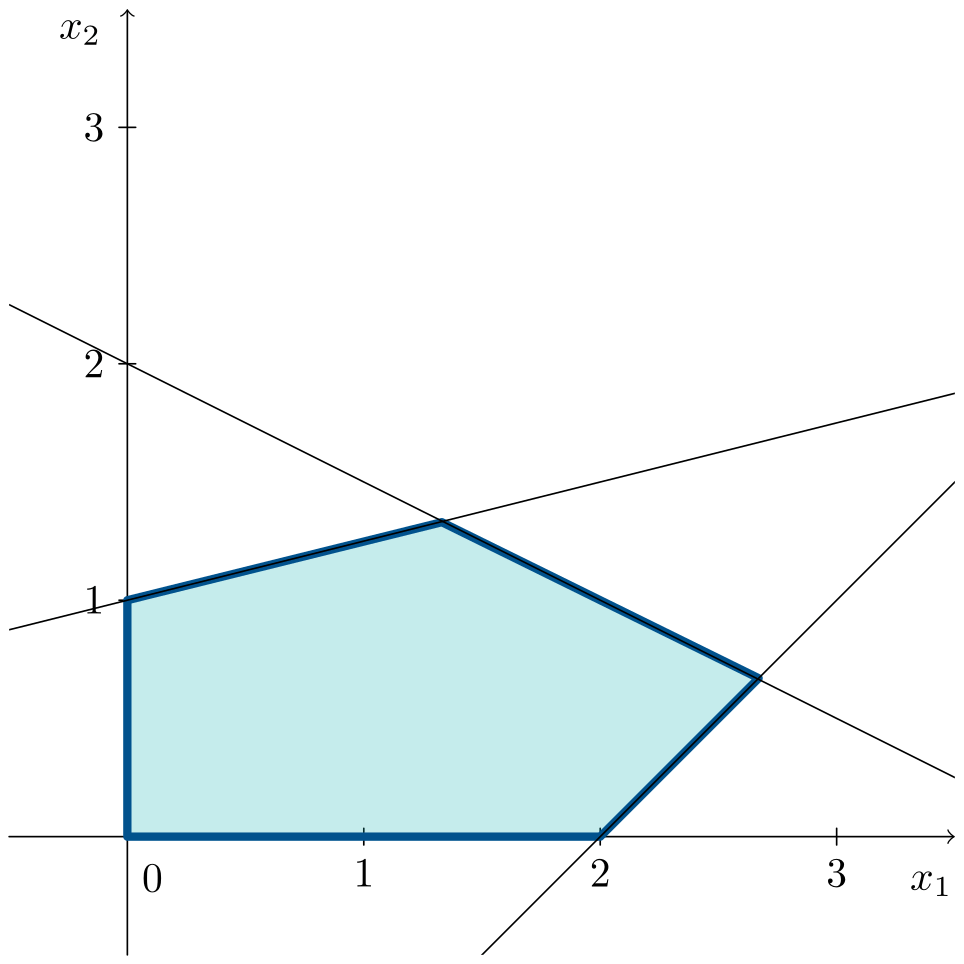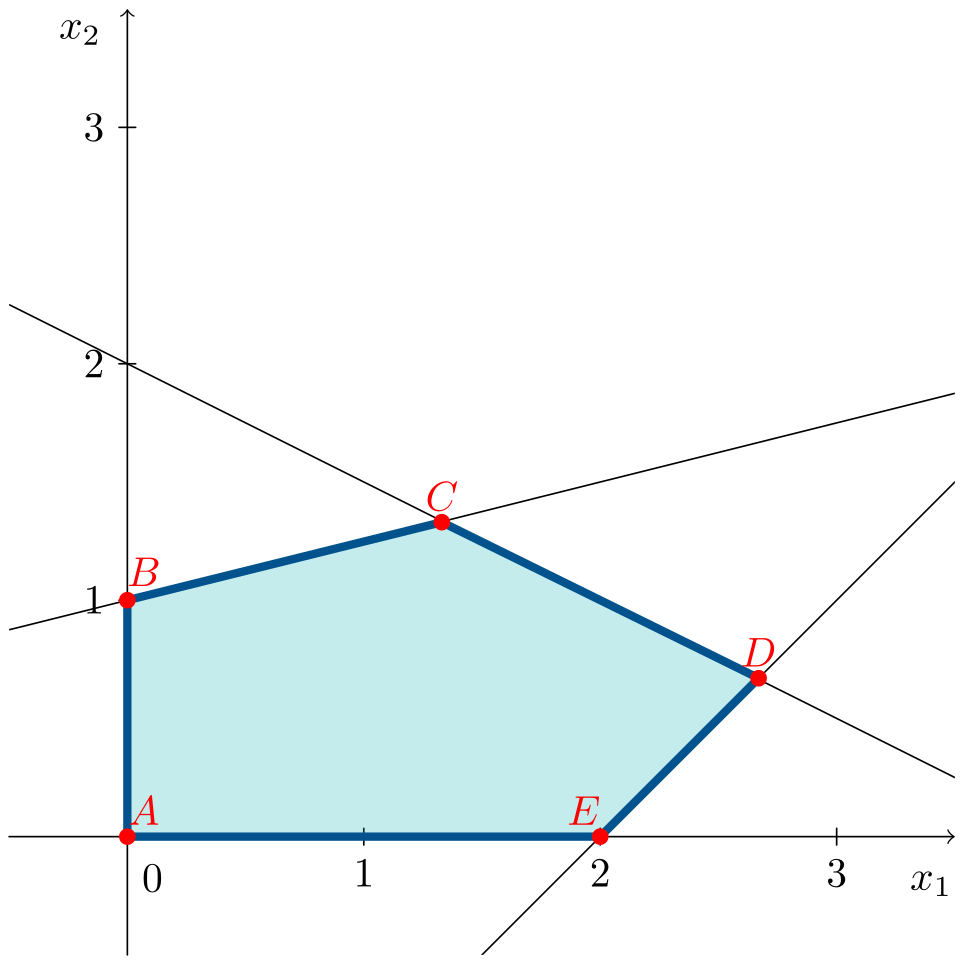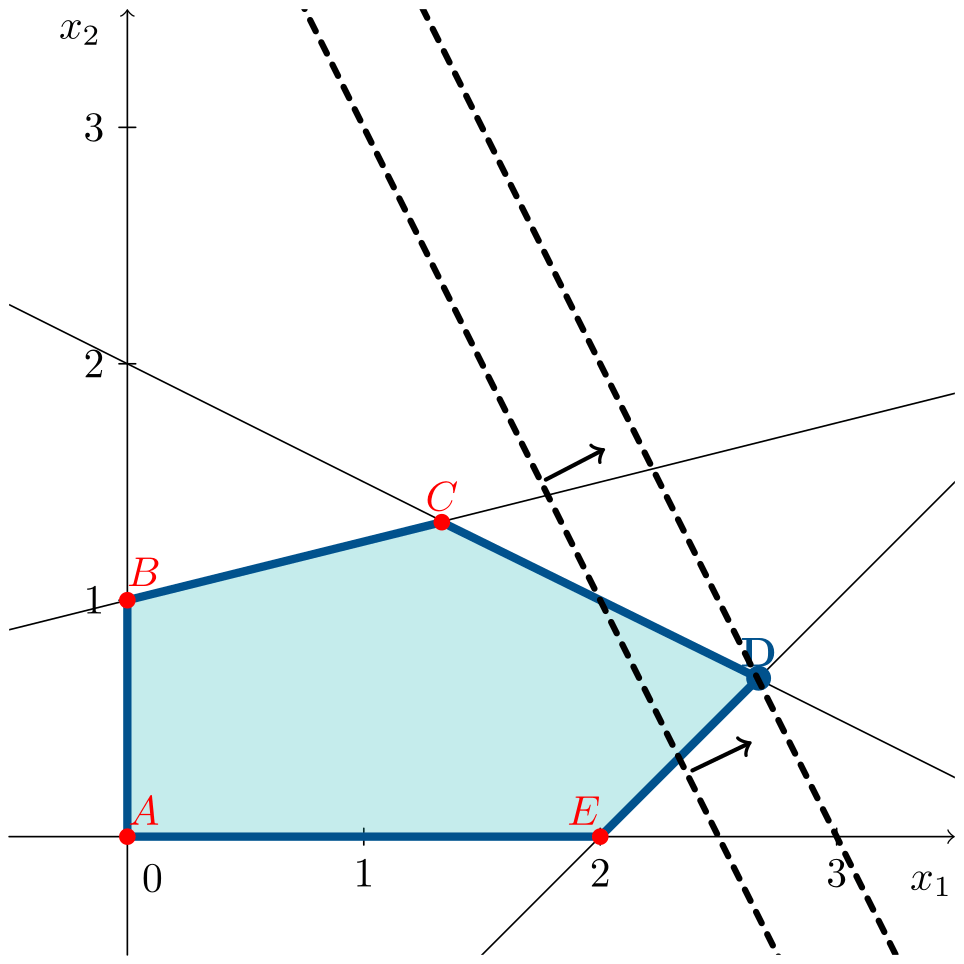
Se puede observar que la solución óptima se encuentra en el vértice $D=(8/3,2/3)^\intercal$ obteniendo un valor en la función objetivo, tras sustituir los valores de $x_1$ y $x_2$, de $z^* = 18$.

Múltiples soluciones óptimas en una región acotada

Sea el siguiente problema de optimización lineal:

\[\begin{aligned} \max\;\;& z = x_1 + x_2 \\ \text{s. a:}\;\;& x_1 + x_2 \leqslant 8 \\ & -4x_1 + 4x_2 \leqslant 8 \\ & 2x_1 - x_2 \leqslant 6 \\ & x_1, x_2 \geqslant 0 \end{aligned}\]

La animación muestra cómo, en este caso, la recta de la función objetivo coincide con un lado completo de la región factible.

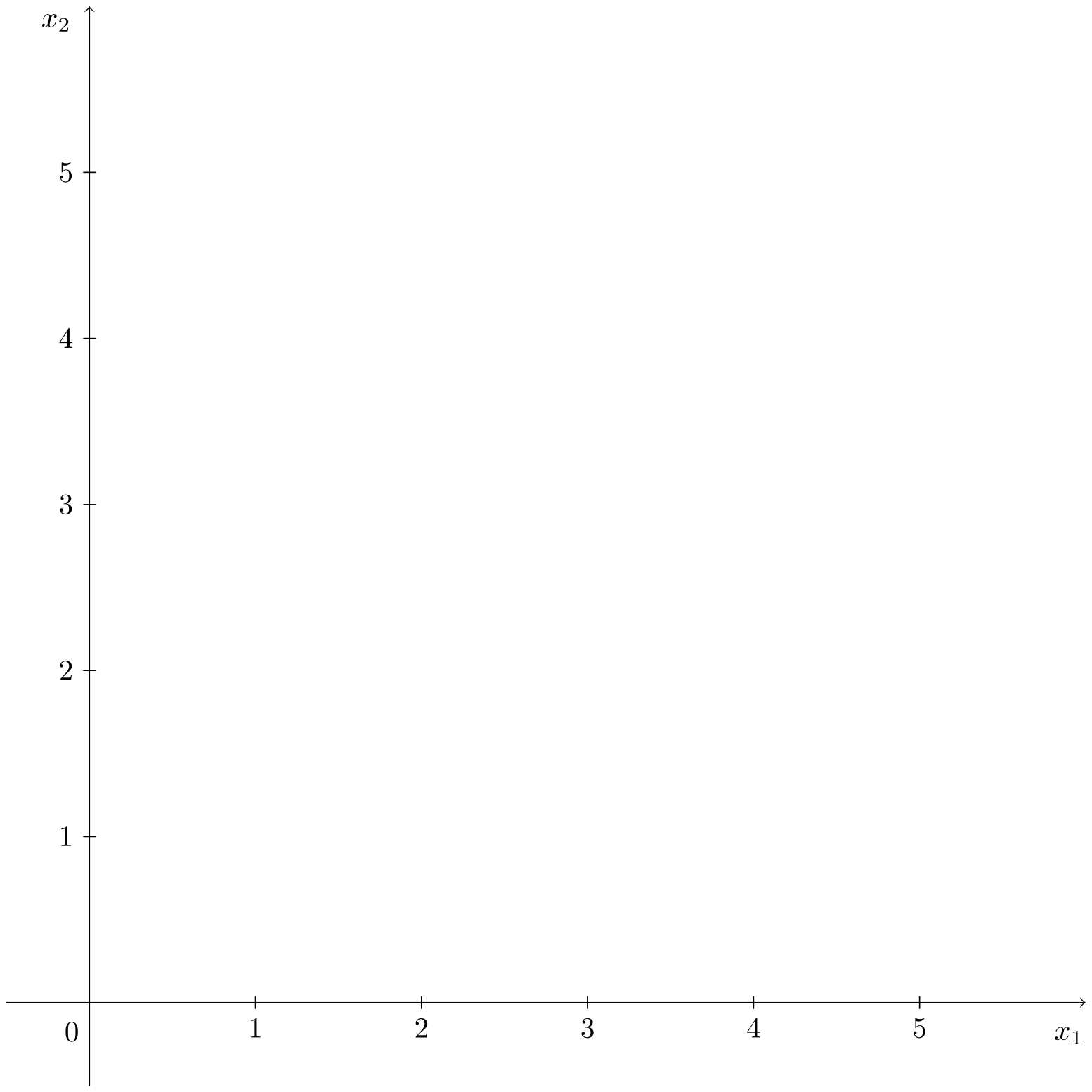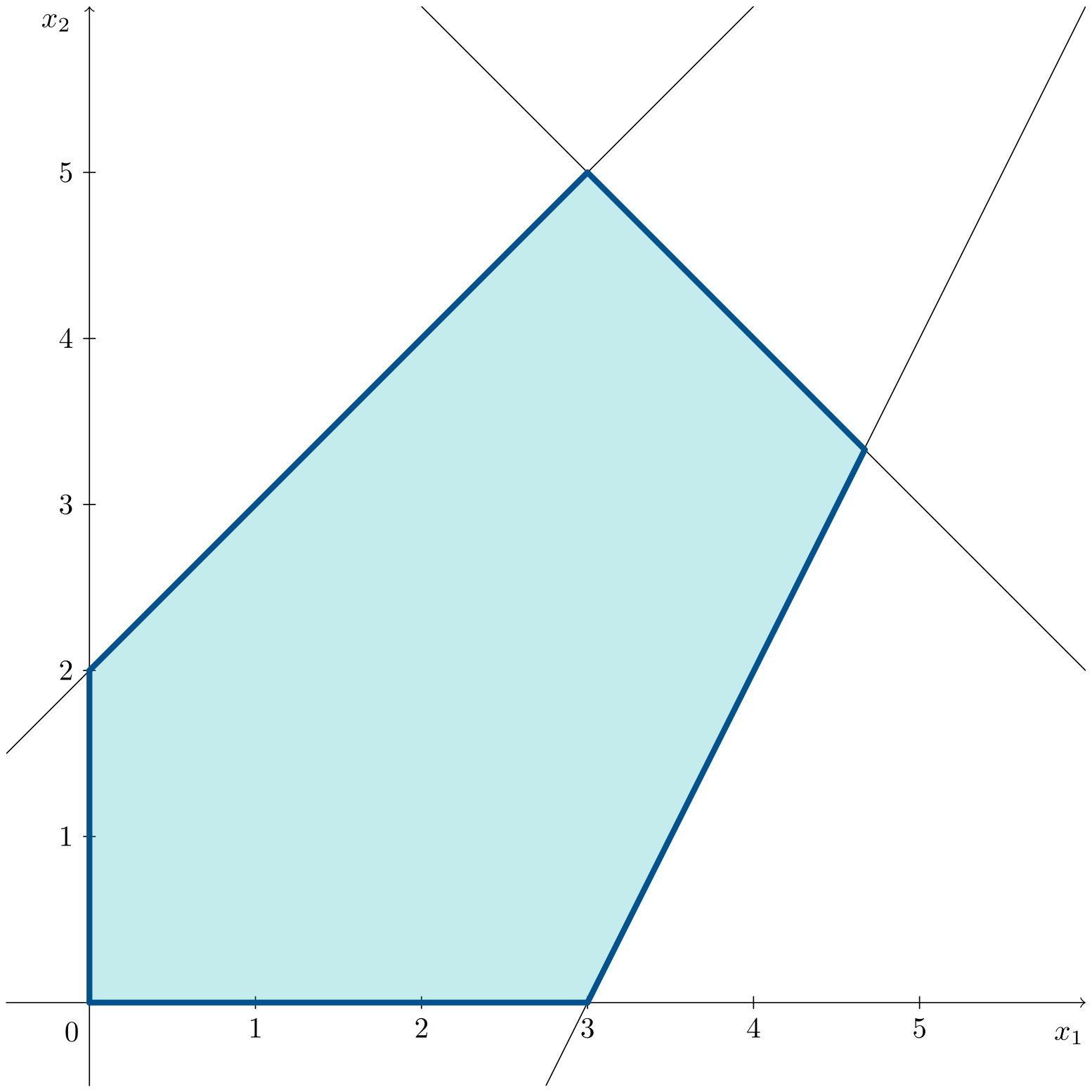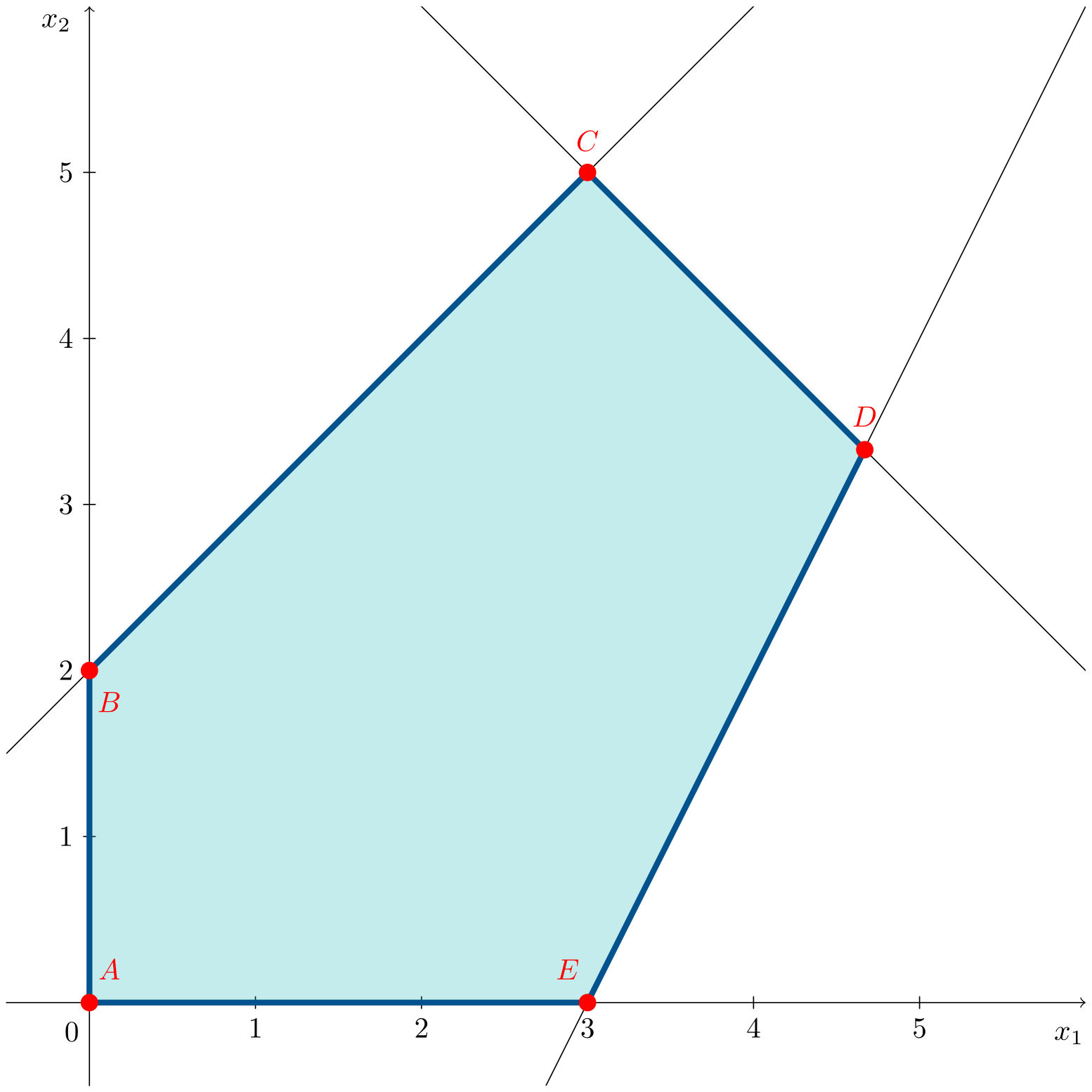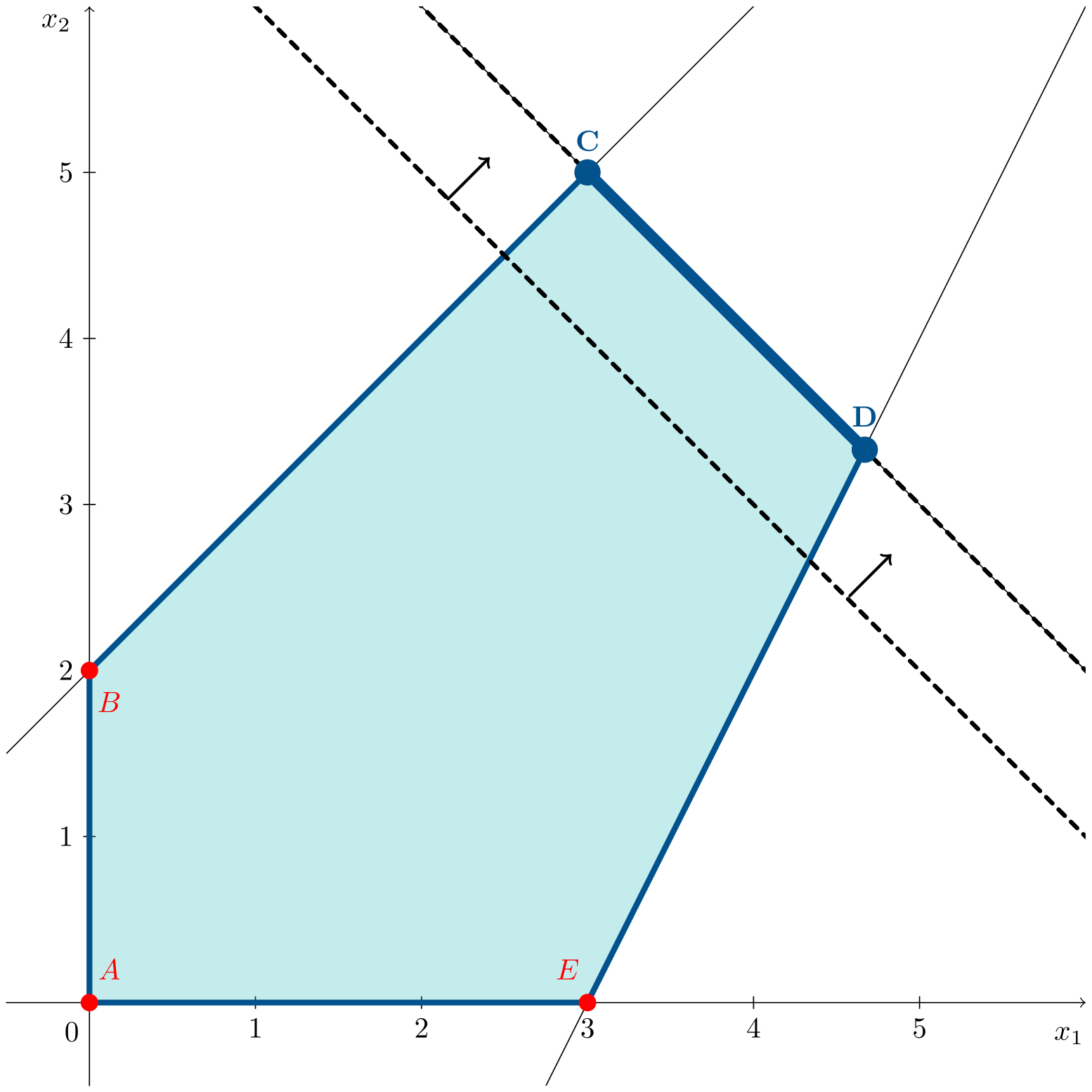
Los vértices $C=(3,5)^\intercal$ y $D=(14/3,10/3)^\intercal$ son soluciones óptimas, además de todos los puntos del segmento que los une. Por tanto, las soluciones óptimas del problema son la combinación lineal convexa entre ambos puntos $C$ y $D$ y vienen dadas por:

\[\lambda \left(\begin{array}{c} 3 \\ 5\end{array}\right) + (1-\lambda) \left(\begin{array}{c} 14/3 \\ 10/3\end{array}\right) \quad \lambda \in [0,1]\]

con un valor de la función objetivo $z^*=8$.

Múltiples soluciones óptimas en una región no acotada

Sea el siguiente problema de optimización lineal:

\[\begin{aligned} \min\;\;& z = x_1 \\ \text{s. a:}\;\;& x_1 - x_2 \leqslant 2 \\ & 2x_1 + 2x_2 \geqslant 1 \\ & x_1, x_2 \geqslant 0 \end{aligned}\]

La animación muestra cómo, en este caso también, la recta de la función objetivo coincide con un lado completo de la región factible.

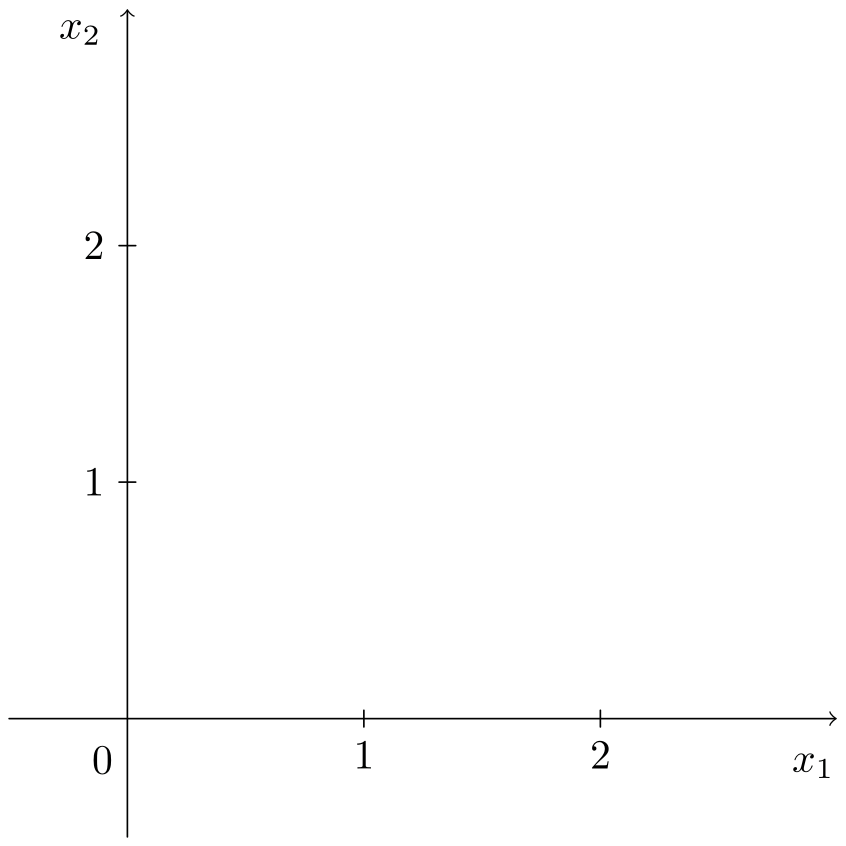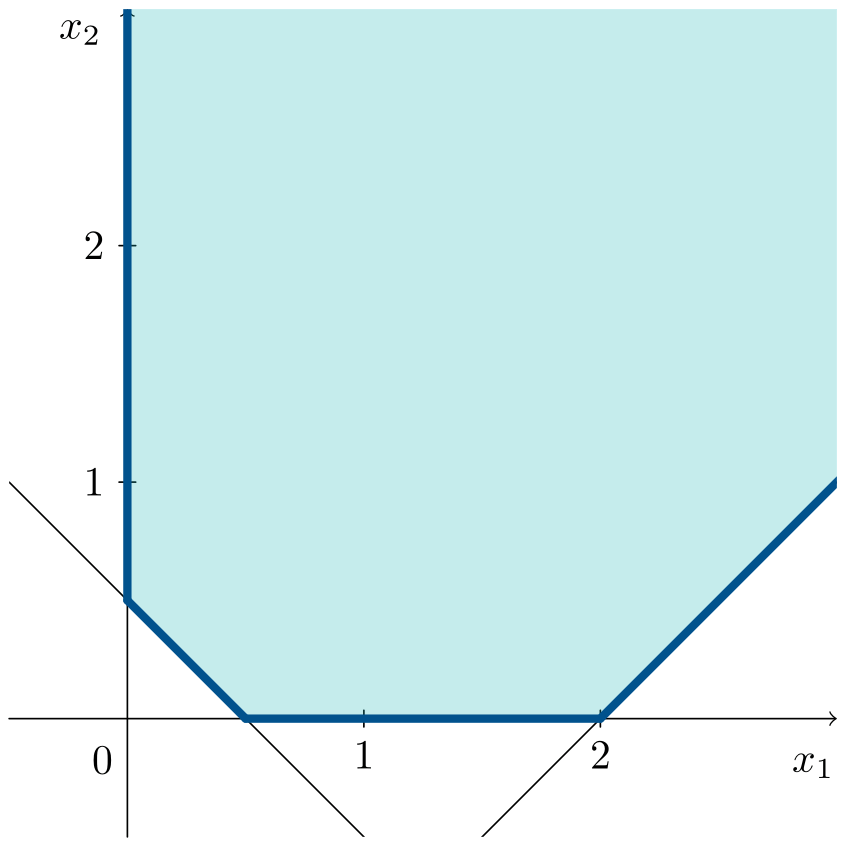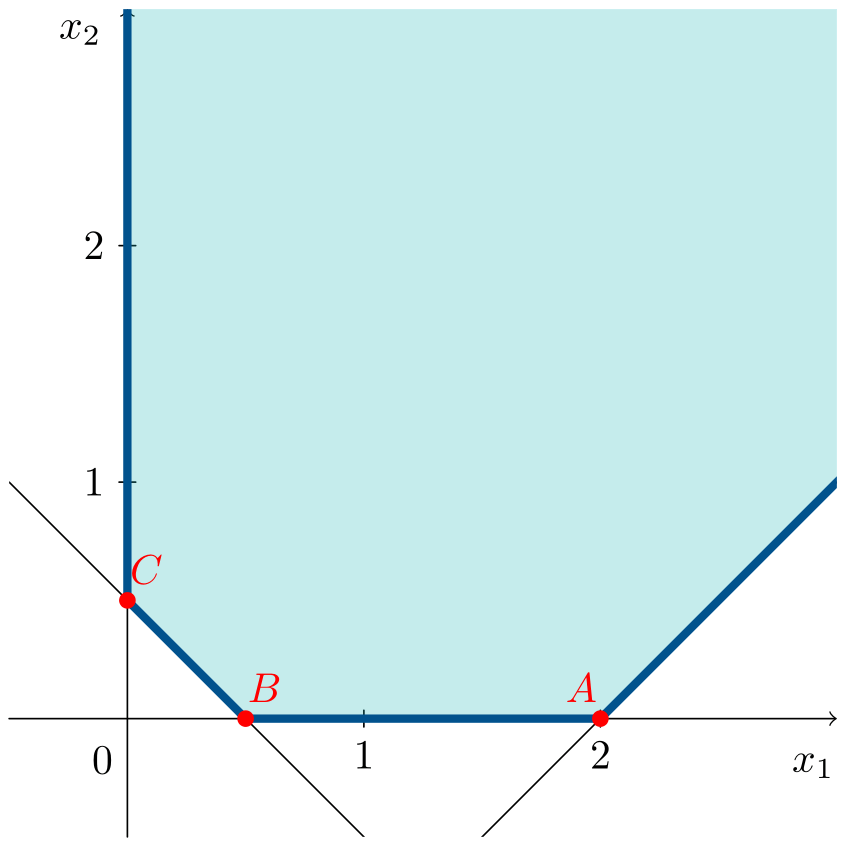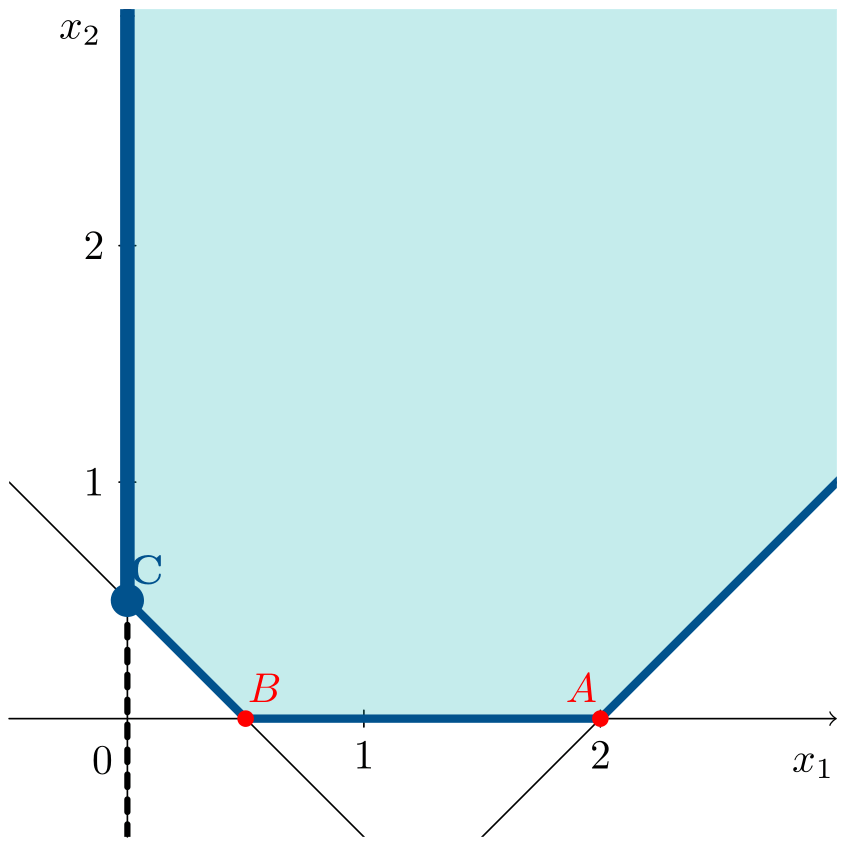
El vértice $C=(0,1/2)^\intercal$ es solución óptima junto al conjunto de puntos que se encuentran en la semirrecta que parte de $C$ hacia la parte positiva del eje de ordenadas. Las soluciones óptimas del problema vienen dadas por:

\[\left(\begin{array}{c} 0 \\ 1/2\end{array}\right) + \mu \left(\begin{array}{c} 0 \\ 1 \end{array}\right) \quad \mu \geqslant 0\]

donde se tiene en cuenta el vértice obtenido y el vector que define la dirección de la semirrecta hacia donde se encuentran las soluciones óptimas del problema, o dirección extrema. Todos estos puntos producen el mismo valor de la función objetivo, $z^*=0$.

Solución óptima no acotada

Sea el siguiente problema de optimización lineal:

\[\begin{aligned} \max\;\;& z = x_1 + 2x_2 \\ \text{s. a:}\;\;& x_1 + 2x_2 \geqslant 2 \\ & -2x_1 + x_2 \leqslant 4 \\ & x_1, x_2 \geqslant 0 \end{aligned}\]

La animación muestra cómo, en este caso, la recta de la función objetivo puede desplazarse mejorando la solución obtenida sin límite.

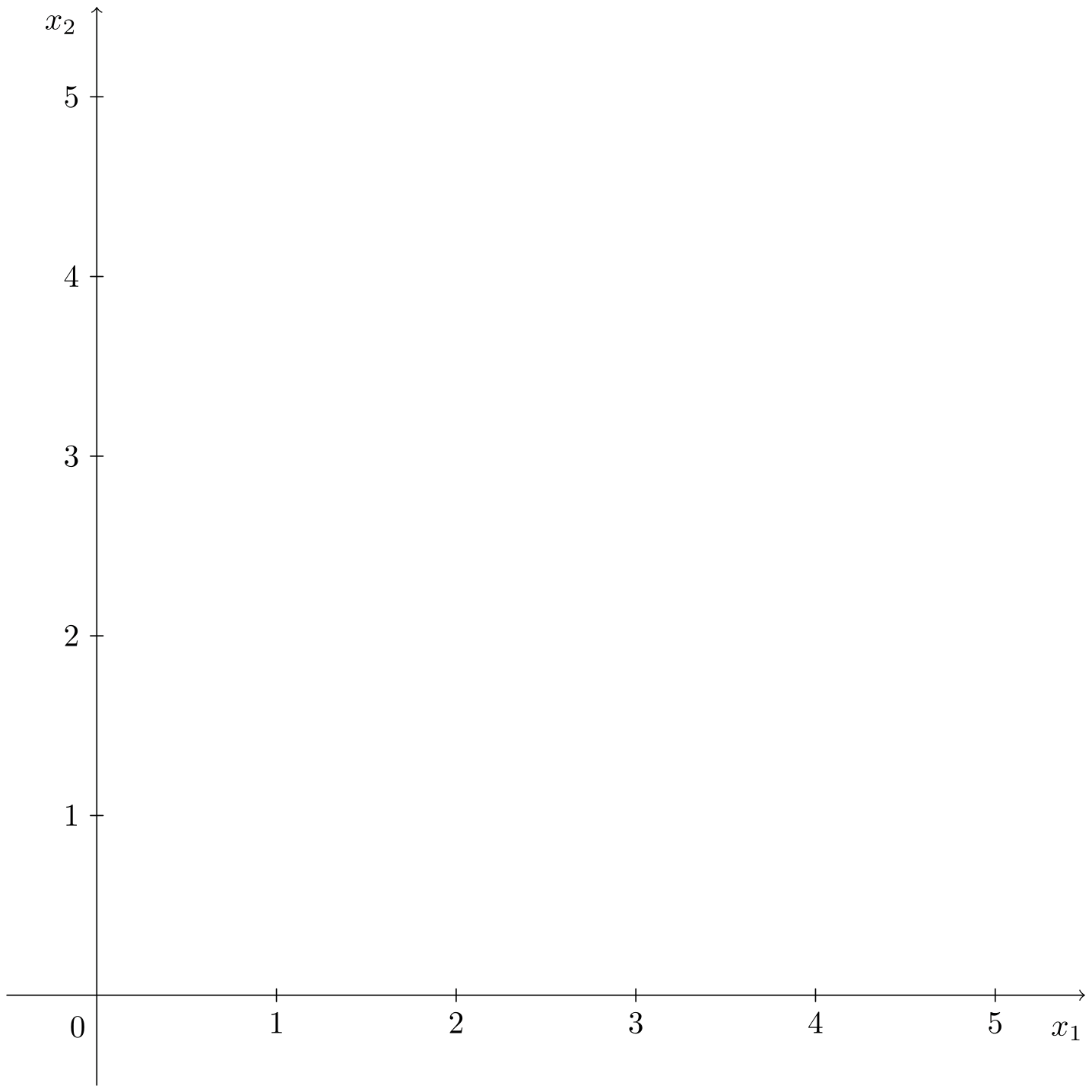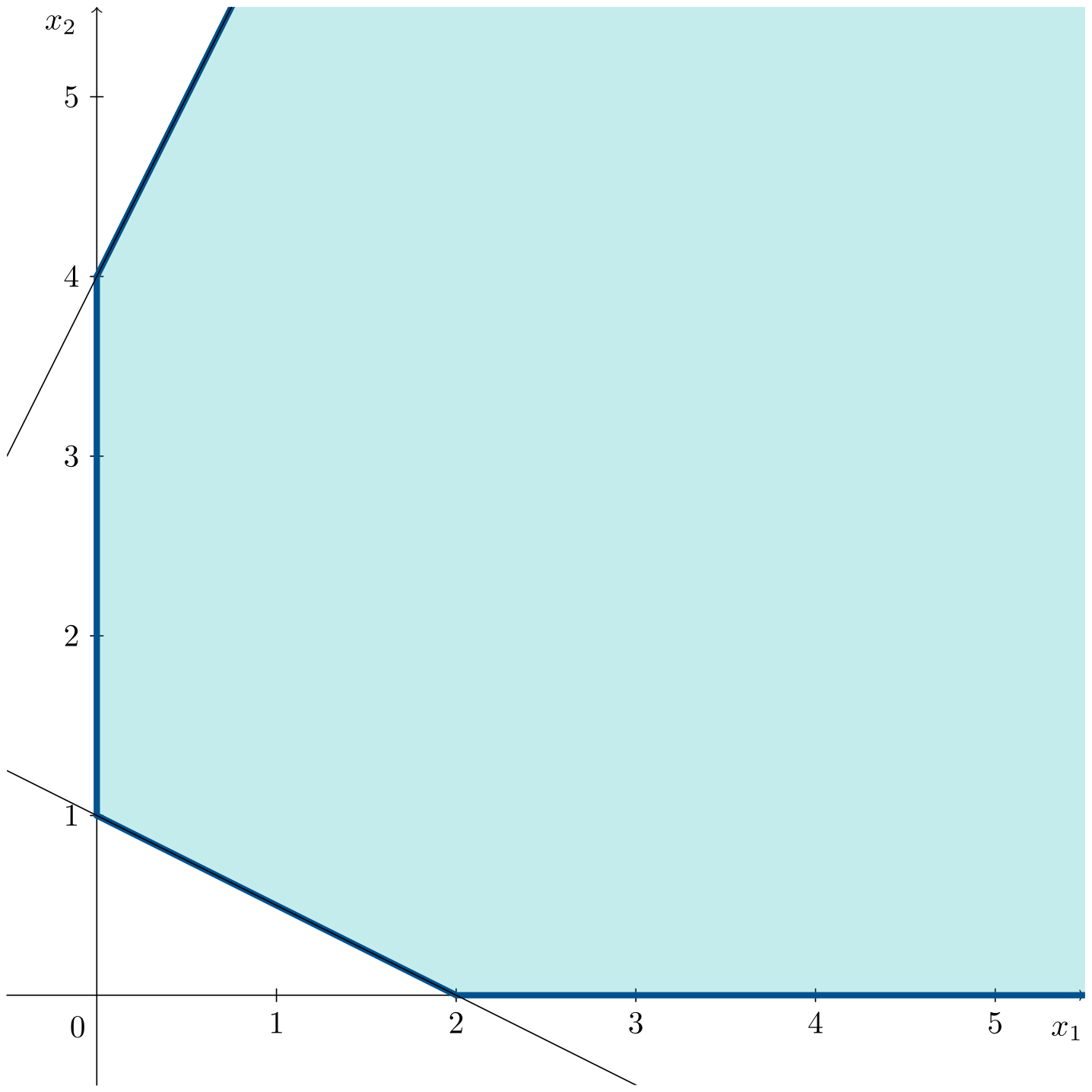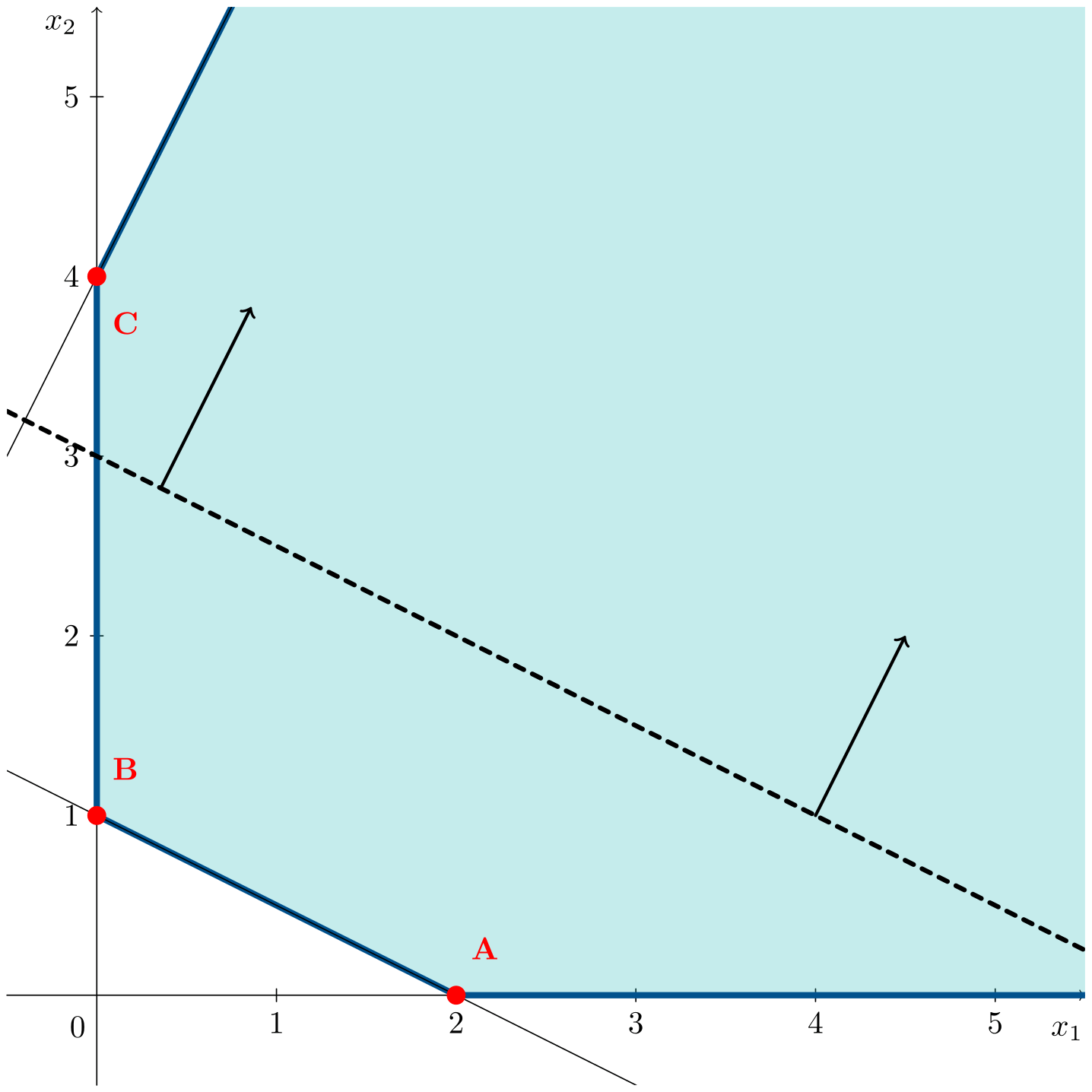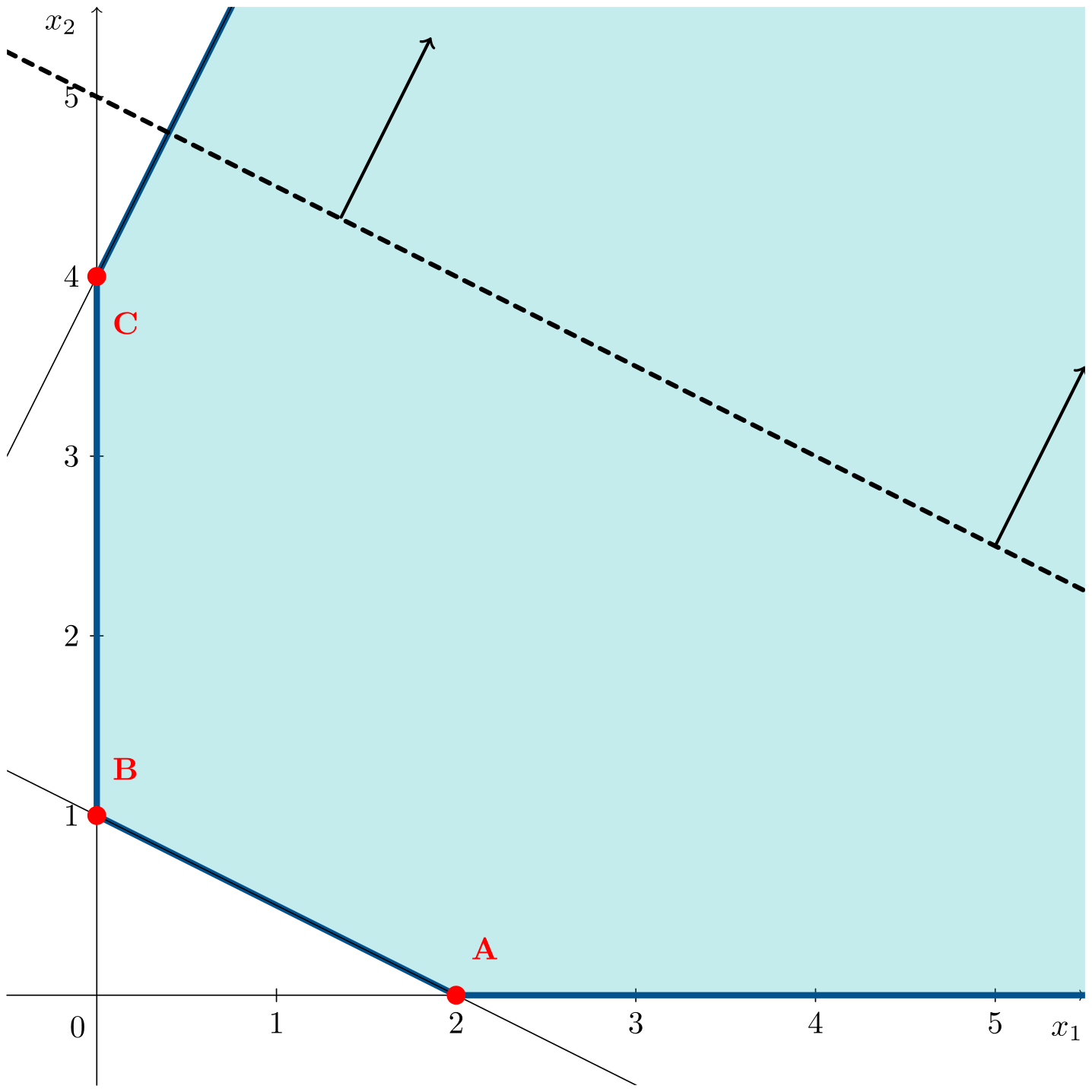
Siguiendo la dirección de mejora de la función objetivo no se llega a ningún vértice pudiendo mejorar la función objetivo tanto como se desee. En este caso, el valor óptimo de la función objetivo es $z^* = \infty$.

Problema infactible

Sea el siguiente problema de optimización lineal:

\[\begin{aligned} \min\;\;& z = x_1 + x_2 \\ \text{s. a:}\;\;& 2x_1 + x_2 \leqslant 5 \\ & x_1 - x_2 \geqslant 4 \\ & x_1, x_2 \geqslant 0 \end{aligned}\]

La animación muestra cómo, en este caso, no hay intersección del primer cuadrante con las dos restricciones planteadas.

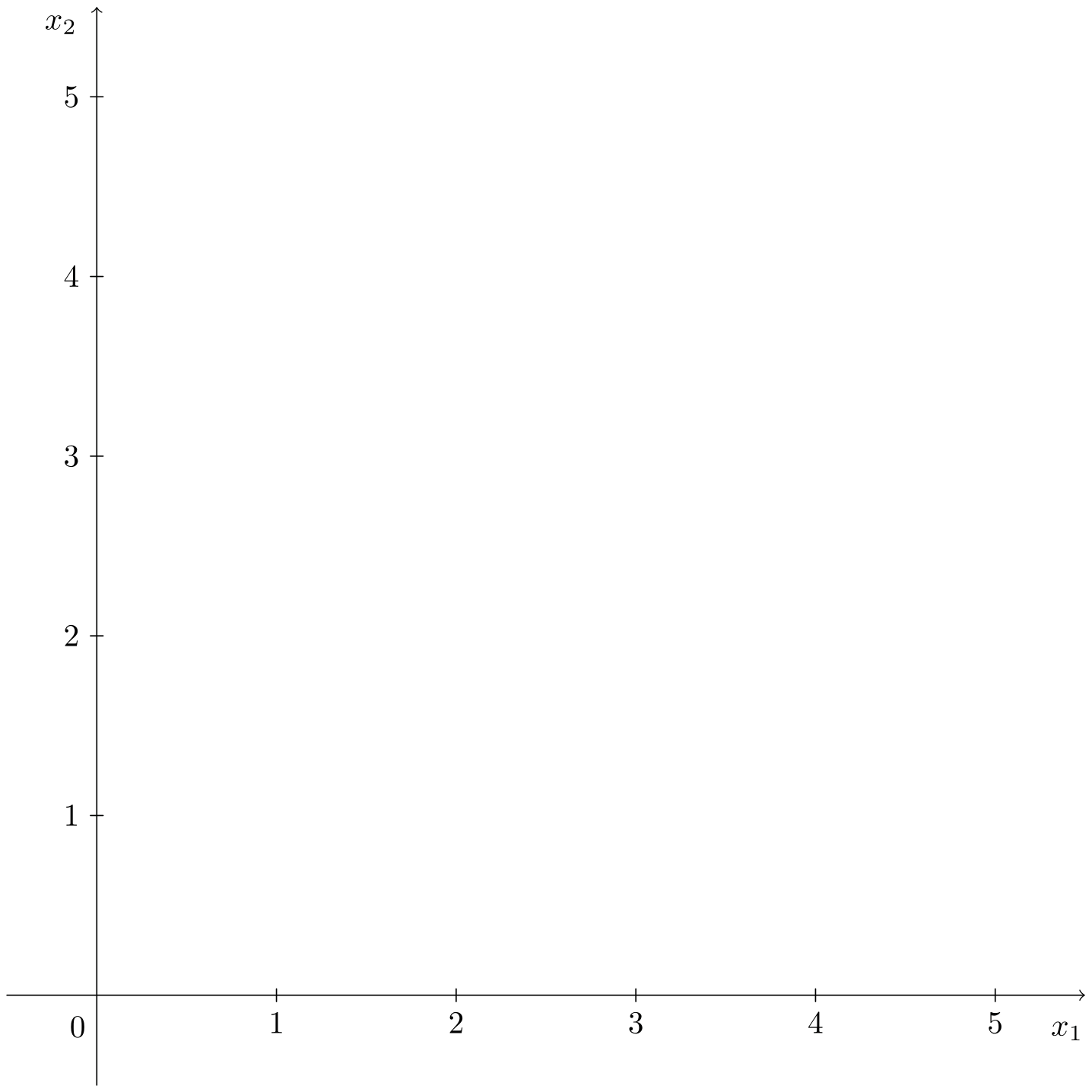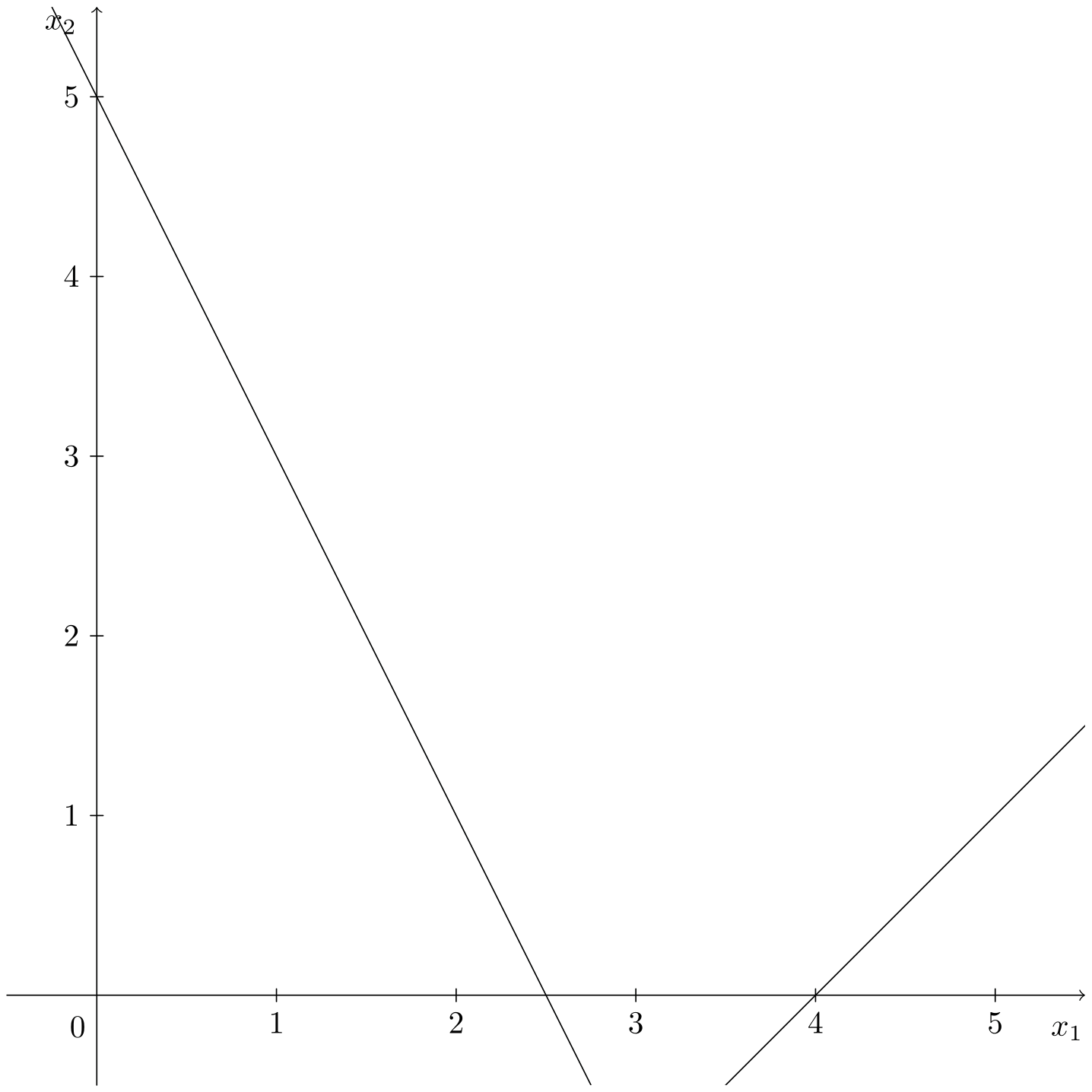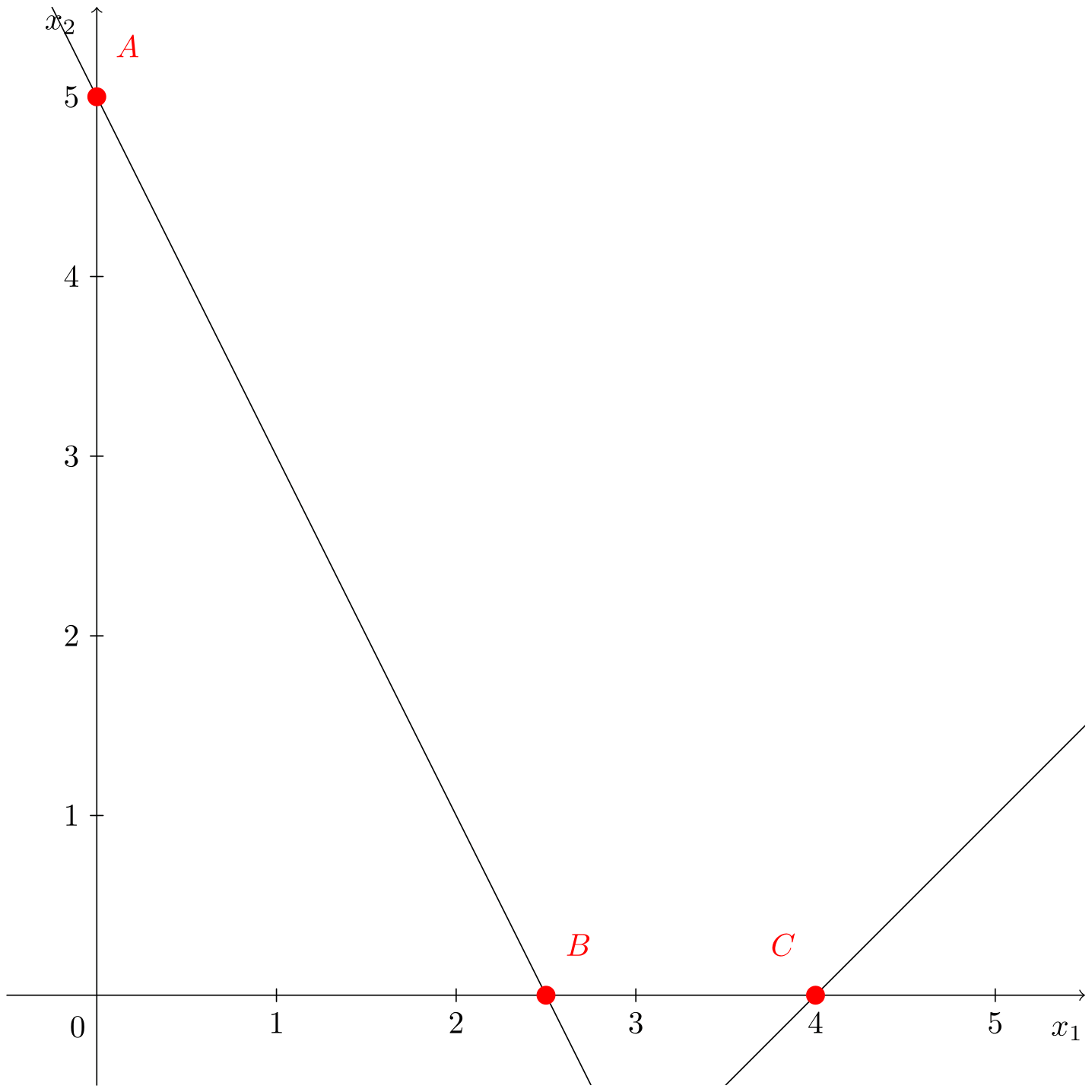
Se observa que la región factible es vacía y, por tanto, el problema es infactible, no existe ninguna solución que satisfaga el conjunto de restricciones del problema.

En todos los casos estudiados se observa que el comportamiento de la solución depende exclusivamente de la geometría de la región factible y de la dirección de la función objetivo. Es importante tener en cuenta que la recta de la función objetivo debe moverse en la dirección correcta en función del criterio de optimización (maximización o minimización) y que no se confundan los términos región no acotada con solución óptima no acotada.

En dos dimensiones, resolver un problema de optimización lineal consiste en:

1. Construir la región factible.
2. Identificar sus vértices y direcciones extremas.
3. Desplazar la recta objetivo en la dirección correcta.
4. Analizar el punto o conjunto de puntos donde se alcanza el óptimo (si existe).

Limitaciones del método gráfico

El enfoque gráfico está limitado a problemas con dos o tres variables de decisión. Para problemas de mayor dimensión se requieren métodos algorítmicos como el Algoritmo del Símplex o Métodos de Punto Interior.

No obstante, la intuición geométrica adquirida en dos dimensiones sigue siendo válida y sirve como base para entender técnicas más avanzadas. Hemos podido observar que:

• Convexidad: El conjunto de soluciones del problema es convexo.
• Vértices o puntos extremos: Son los puntos potencialmente candidatos a ser la solución óptima del problema a resolver.
• Direcciones extremas: Se dan en problemas cuya región factible no es acotada, permitiendo definir el conjunto de soluciones óptimas (en caso de multiplicidad de óptimos) o la dirección de mejora cuando se obtiene solución óptima no acotada.
• Tipos de solución: Se pueden obtener diferentes conclusiones al resolver el problema.

El método gráfico proporciona una forma clara e intuitiva de entender la optimización lineal. Comprender este método es un primer paso importante hacia herramientas de optimización más generales y potentes. Estas ideas geométricas son las que permiten generalizar el razonamiento a métodos como el Símplex, donde ya no es posible dibujar el problema, pero sí razonar sobre vértices y direcciones extremas.